The Similarity Ratio
How would your students solve the following problem? (After they discuss their love or hatred of clowns, that is.) A clown’s face on a balloon is 4 in. high when the balloon holds 108 in.3 of air. How much air must the balloon hold for the face to be 8 in. high?
My students try to take the given measurements and make a proportion out of them. For several years now, I have tried to figure out a way to help students not just understand that the areas and volumes of two similar figures are not proportional to their side lengths (or perimeters) but know how to apply that concept to solve problems.
This year we started with the Soccer Ball Inflation video on 101 Questions.
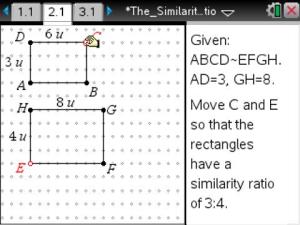
Then we explored what happened with similar rectangles – their similarity ratios, perimeters, and areas.
We summarized the results:
And then moved to right triangles.
And then we worked problems similar to the clown problem, uncovering misconceptions, figuring out the incorrect thinking that occurred for incorrect responses.
And the results on the summative assessment were better than usual. Last year, on a problem like the clown problem, less than 50% of students answered it correctly. This year, 72% answered it correctly.
And so, the journey continues, where some years the results are better than others …
Easing the Hurry Syndrome 
Amy Zimmer
December 30, 2015 at 7:01 pm
Hi Jennifer,
I am looking for a great lesson to start dilation and similarity for the new semester.
I am really excited about the soccer ball modeling project. I noticed that on one of your posts you mentioned that you completed lesson 6A, 6B, 6C, etc…
Can you please tell me what these reference?
We have covered congruence, but now I see that next year we may need to look at congruence as a special circumstance of similarity.
Thank you for all the good information.
Amy
jwilson828
December 31, 2015 at 9:27 am
Hi, Amy.
We started with Notice & Note on Dilations (A): https://easingthehurrysyndrome.wordpress.com/2015/11/17/notice-and-note-dilations/
Then we did Similarity Theorems (B):
https://easingthehurrysyndrome.wordpress.com/2014/01/26/similarity-theorems/
This year for C we did a formative assessment lesson from the Mathematics Assessment Project (normally you do these later in the unit, but because our students come with some experience with this content from middle school, we did it earlier rather than later):
http://map.mathshell.org/lessons.php?unit=9320&collection=8&redir=1
Did you see the Soccer Ball Inflation post? That might be a good way to start the unit with best guesses, even if they actually solve/calculate later in the unit.
https://easingthehurrysyndrome.wordpress.com/2015/12/13/soccer-ball-inflation/
Happy New Year!