Several students noted in their reflection on our circles unit that the performance assessment tasks helped them “combine everything that we learned to find the correct answers to challenging problems”.
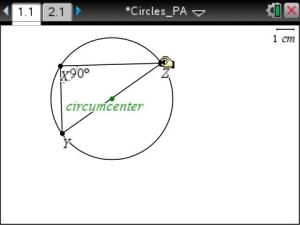
We started with a diagram from the Mathematics Assessment Project formative assessment lesson. Inscribing and Circumscribing Right Triangles
and asked students to
1. Figure out the radii of the circumscribed circle for a right triangle with sides 5 units, 12 units and 13 units. Show and justify every step of your reasoning.
2. Use mathematics to explain carefully how you can figure out the radii of the circumscribed circle of a right triangle with sides of any length: a, b and c (where c is the hypotenuse).
The second task provided a bit more structure. Circles in Triangles comes from a Mathematics Assessment Project apprentice task.
Students were given the following:
This diagram shows a circle that just touches the sides of a right triangle whose sides are 3 units, 4 units, and 5 units long.
1. Prove that triangles AOX and AOY are congruent.
2. What can you say about the measures of the line segments CX and CZ?
3. Find r, the radius of the circle. Explain your work clearly and show all your calculations.
I wonder what would have happened if we had asked students to determine the radius of the inscribed circle without as many auxiliary lines already given in the figure? Instead, what if we had used the same figure as the first task?
Another teacher taught this lesson to my students. She saved their work for me because even with the auxiliary lines drawn, students made sense of the structure (and particularly the expressions they wrote for the segment lengths) in different ways.
Then they were asked to determine the radius of the inscribed circle for a 5, 12, 13 right triangle, and then they were asked to generalize their results.
This diagram shows a circle that just touches the sides of a right triangle whose sides are 5 units, 12 units, and 13 units long.
4. Draw construction lines as in the previous task, and find the radius of the circle in this 5, 12, 13 right triangle. Explain your work and show your calculations.
5. Use mathematics to explain carefully how you can figure out the radii of the inscribed circle of a right triangle with sides of any length: a, b and c (where c is the hypotenuse).
I wonder how technology fits in with tasks like these?
We had a skeleton of a diagram prepared for students who wanted to use it.
Students had to measure themselves for the construction to be helpful in making sense of the mathematics. I find that the technology can be helpful for those who don’t know where to start. What do you notice when the triangle is right?
Can it help them reason abstractly and quantitatively, starting with the quantitative and building to generalization? Can it help them make sense of problems and persevere in solving them, when they don’t know what else to do on paper?
We also had a skeleton of a diagram prepared for the inscribed circle for those who wanted to use it.
What auxiliary lines (or segments) would you construct and measure for the inscribed circle?
The technology can help them make a conjecture about the length of the radius, and then they can go back to the mathematics to help them understand why.
And so the journey continues … Maybe some year I will be brave enough to start our Circles unit with this task and let the mathematics unfold in the context of the task as it is needed.








Travis
March 14, 2014 at 5:33 pm
No bravery needed…merely post this on the wall for those who are inclined. At least for the first time….baby steps. ‘Theme’ problems are great motivators for some students. CPM math does this well.