#NCTMLive and #T3Learns webinar: Implement tasks that promote reasoning and problem solving, and use and connect mathematical representations.

On Wednesday, May 2, 2018, Jill Gough (@jgough) and I co-facilitated the second webinar in a four-part series on the Eight Mathematics Teaching Practices from NCTM’s Principles to Actions: Ensuring Mathematical Success for All.

---

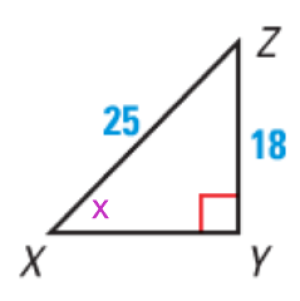
Implement tasks that promote reasoning and problem solving,
and Use and connect mathematical representations.

Effective teaching of mathematics facilitates discourse among learners to build shared understanding of mathematical ideas by analyzing and comparing approaches and arguments.

• How might we implement and facilitate tasks that promote productive discussions to strengthen the teaching and learning of mathematics in all our teaching settings – teaching students and teaching teachers?
• What types of tasks encourage mathematical flexibility to show what we know in more than one way?

Our slide deck:

View this document on Scribd

View this document on Scribd

Our agenda:

7:00	Jill/Jennifer’s Opening remarks Share your name and grade level(s) or course(s). Norm setting and Purpose
7:05	Number Talk: 81 x 25 Your natural way and Illustrate Decompose into two or more addends (show it) Show your work so a reader understands without asking questions Share work via Twitter using #NCTMLive or bit.ly/nctmlive52
7:10	#LL2LU Use and connect mathematical representations Self-assess where you are Self-assessment effect size Think back to a lesson you taught or observed in the past month. At what level did you or the teacher show evidence of using mathematical representations?
7:15	Task:  (x+1)^2 does/doesn’t equal x^2+1
7:25	Taking Action (DEI quote)
7:30	#LL2LU Implement Tasks That Promote Reasoning and Problem Solving
7:35	Graham Fletcher’s Open Middle Finding Equivalent Ratios
7:45	Illustrative Mathematics: Jim and Jesse’s Money
7:55	Close and preview next in the series

Some reflections from the chat window:

I learned to pay attention to multiple representations that my students will create when they are allowed the chance to think on their own. I learned to ask myself how am I fostering this environment with my questioning.

I learned to pay attention to the diversity of representations that different students bring to the classroom and to wait to everyone have time to think

I learned to pay attention (more) to illustrating work instead of focusing so much on algebraic reasoning in my approach to teaching Algebra I. I learned to ask myself how could I model multiple representations to my students.

I learned to pay attention to multiple representations because students all think and see things differently.

I learned to make sure to give a pause for students to make the connections between different ways of representing a problem, rather than just accepting the first right answer and moving on.

I learned to pay attention to the ways that I present information and concepts to children… I need to include more visual representations when I working with algebraic reasoning activities.

---

Cross-posted on Experiments in Learning by Doing

 

Webinar: Establish Mathematics Goals to Focus Learning, and Elicit and Use Evidence of Student Thinking.

On Wednesday, March 28, 2018, Jill Gough (@jgough) and I co-facilitated the first webinar in a four-part series on the Eight Mathematics Teaching Practices from NCTM’s Principles to Actions: Ensuring Mathematical Success for All.

Establish Mathematics Goals to Focus Learning, and Elicit and Use Evidence of Student Thinking.

Effective teaching of mathematics uses evidence of student thinking to assess progress toward mathematical understanding and to adjust instruction continually in ways that support and extend learning.

• How might we communicate with clarity to ensure that learners are focused on high quality mathematical goals?
• What types of tasks provide opportunities for learners to notice, note, wonder, and take action as agents of their own learning?

Jill’s sketch note of our plan:

Our slide deck:

View this document on Scribd

Agenda:

7:00	Opening remarks Share your name and grade level(s) or course(s). – Maybe a poll? Norm setting and Purpose
7:05	Establish mathematics goals to focus learning #LL2LU Hattie: Teacher Clarity Hattie: I can statements – specific #LL2LU
7:10	Task:  Illustrative Math – Fruit Salad? Demonstrate flexibility Look for and make use of structure Share your work via Twitter using #NCTMLive or http://bit.ly/IMfruitsalad-dropyourwork
7:25	Quotes from Taking Action
7:30	Elicit and use evidence of student thinking #LL2LU Dylan Wiliam James Popham #LL2LU
7:35	Let’s Do Some Math Robert Kaplinsky: Open Middle Biggest Product ?
7:45	Talking Points – Elizabeth Statmore Suggestion One talking about learning math Suggestion Two talking about mathematics Geometry Talking Points example Ratios and Proportional reasoning Talking Points example Here’s the bank of talking points
7:55	Close and preview next in the series

Some reflections from the chat window:

• I learned to pay attention to how my students may first solve the problem or think about it prior to me teaching it to try and see connections that are made or how I can meet them. ~C Heikkila
• I learned how to pay attention to how I introduce tasks to students. Sometimes I place limits on their responses by telling them what I expect to see in their responses as it relates to content topics. I will be more mindful about task introduction. ~M Roland
• I learned to pay more attention to mathematical operations, and to look for more solutions that can satisfy the given problem. ~B Hakmi
•  I also learned the importance of productive struggle and to be patient with my students. ~M James
• I’m thinking about how to encourage my teachers to intentionally teach the mathematical practices. ~M Hite
• I learned to pay attention to the learning progressions so I can think of the work as a process and journey. ~B Holden
• A new mathematical connection for me was the idea of graphing values for the product example. ~A Warden
• I learned to pay attention to peer discussions to discover how well students are learning the concepts. ~M Grech
• Am I anticipating the roadblocks to learning? ~L Hendry

An audio recording of the webinar and the chat transcript can be viewed at NCTM’s Partnership Series.

Cross posted at Experiments in Learning by Doing

 

I can establish mathematics goals to focus learning

We strive to grow in our understanding of the Eight Mathematics Teaching Practices from NCTM’s Principles to Actions: Ensuring Mathematical Success for All. This research-informed framework of teaching and learning reflects a core set of high leverage practices and essential teaching skills necessary to promote deep learning of mathematics.

Establish mathematics goals to focus learning.

Effective teaching of mathematics establishes clear goals for the mathematics that students are learning, situates goals within learning progressions, and uses the goals to guide instructional decisions.

In order to support our teaching teams as they stretch to learn more, we drafted the following learning progressions. We choose to provide a couple of pathways to focus teacher effort, understanding, and action.

When working with teacher teams to establish mathematics goals to focus learning, we refer to 5 Practices for Orchestrating Productive Mathematics Discussions by Peg Smith and Mary Kay Stein and Visible Learning for Mathematics, Grades K-12: What Works Best to Optimize Student Learning by John Hattie, Douglas Fisher, and Nancy Frey along with Principles to Actions: Ensuring Mathematical Success for All by Steve Leinwand.

To deepen our understanding around establishing mathematics goals, we anticipate, connect to prior knowledge, explain the mathematics goals to learners, and teach learners to use these goals to self-assess and level up.

From  NCTM’s 5 Practices for Orchestrating Productive Mathematics Discussions, we know that we should do the math ourselves, predict (anticipate) what students will produce, and brainstorm what will help students most when in productive struggle and when in destructive struggle.

Once prior knowledge is activated, students can make connections between their knowledge and the lesson’s learning intentions. (Hattie, 44 pag.)

To strengthen our understanding of using mathematics goals to focus learning, we make the learning goals visible to learners, ask assessing and advancing questions to empower students, and listen and respond to support learning and leveling up.

Excellent teachers think hard about when they will present the learning intention. They don’t just set the learning intentions early in the lesson and then forget about them. They refer to these intentions throughout instruction, keeping students focused on what it is they’re supposed to learn. (Hattie, 55-56 pag.)

How might we continue to deepen and strengthen our ability to advance learning for every learner?

What if we establish mathematics learning goals to focus learning?

Cross posted on Experiments in Learning by Doing

---

Hattie, John A. (Allan); Fisher, Douglas B.; Frey, Nancy; Gojak, Linda M.; Moore, Sara Delano; Mellman, William L.. Visible Learning for Mathematics, Grades K-12: What Works Best to Optimize Student Learning (Corwin Mathematics Series). SAGE Publications. Kindle Edition.

Leinwand, Steve. Principles to Actions: Ensuring Mathematical Success for All. Reston, VA.: National Council of Teachers of Mathematics, 2014. (p. 21) Print.

Stein, Mary Kay., and Margaret Smith. 5 Practices for Orchestrating Productive Mathematics Discussions. N.p.: n.p., n.d. Print.

 

Trig Ratios

How do your students experience learning right triangle trigonometry? How do you introduce sine, cosine, and tangent ratios to them?

NCTM’s Principles to Actions includes build procedural fluency from conceptual understanding as one of the Mathematics Teaching Practices. In what ways can technology help us help our students build procedural fluency from conceptual understanding?

Until I started using TI-Nspire Technology several years ago, right triangle trigonometry is one topic where I felt like I started and ended at procedural fluency. How do you get students to experience trig ratios?

I’ve been using the Geometry Nspired activity Trig Ratios ever since it was published. Over the last year, I also read posts from Mary Bourassa: Calculating Ratios and Jessica Murk: Building Trig Tables about learning experiences for making trigonometric ratios more meaningful for students. Here’s how this year’s lesson played out …

We first established a bit of a need for something called trig (when they finally get to learn about the sin, cos, and tan buttons on their calculator that they’ve not known how to use). I showed a diagram and asked how we could solve it. We reserved “trig” for something they couldn’t yet solve.

We use TI-Nspire Navigator with our TI-Nspire handhelds, and so I can send Quick Polls to assess where students are. Sometimes Quick Polls aren’t actually so “quick”, but these were, along with letting students think about what we already know and uncovering a few misconceptions along the way (25 isn’t the same thing as 18√2).

Next I asked each student to construct a right triangle with a 40˚ angle and measure the sides of the triangle.

I sent a Quick Poll to collect their measurements.

Then we looked at the TNS document for Trig Ratios. Students can take multiple actions on the diagram. I asked them to start by moving point B. What do you notice? We recorded their statements for our class notes.

Then I asked them to click on the up and down arrows of the slider. What do you notice?

What ratio of side lengths is used for the sine of an angle?

You all constructed a right triangle with a 40˚ angle and recorded the measurements. What’s true about all of your triangles?

• The triangles are all similar because the angles are congruent.
• The corresponding side lengths are proportional.
• We know that sin(40˚) is always the same.
• So the opposite leg over the hypotenuse will be the same?

Will it? We sent their data to a Lists & Spreadsheet page and calculated a fourth column, opp_leg/hyp. What do you notice?

Of course their ratios aren’t exactly the same, but that’s another good discussion. They are close. And students noticed that one entry has the opposite leg and adjacent leg switched because the leg opposite 40˚ is shorter than the leg opposite 50˚.

We didn’t spend long looking at the TNS pages for tangent and cosine … students were well on their way to understanding a trig ratio conceptually. They just needed to establish which side lengths to use for cosine and which to use for tangent.

There’s a reason that #AskDontTell has been running through my mind as I have conversations with my students and reflect on them. Jill Gough wrote a post using that hashtag over two years ago: Circle Investigation – #AskDontTell.

What #AskDontTell opportunities can you provide your students this week?

[Cross-posted at T3 Learns]

 

Infestation to Extermination

We used a problem from the Calculus Nspired activity Infestation to Extermination recently during our unit on differential equations:

The rate of increase of bugs is proportional to the number of bugs in a certain area. When t=0, there are 2 bugs and they are increasing at a rate of 3 bugs/day.

What does this mean?

I set the mode to individual and watched as students worked.

Many recognized that the rate of change changes.

Several used the initial condition to write a statement about the rate of change.

Eventually, we went back to the given information to decipher what it was saying.

And then we (anti)derived the model for exponential growth, which of course students recognized using in a previous math course.

So what are the constants for this particular model?

I sent a poll to collect their model honestly having no idea that the bell was going to ring in less than two minutes. A few students correctly answered before the end of class.

Productive struggle isn’t fast.

I should have paid better attention to the time … I really had no idea it had taken us as long as it did. But students were engaged in “grappling with mathematical ideas and relationships” the entire time. That’s got to be better for their learning than them watching me tell them how to work the problem.

What opportunities are you giving your students to struggle productively? Even if you don’t “cover” as much as you think you should?

And so the #AskDontTell journey continues …

 

Area between Curves

Our learning goals for the Applications of Definite Integrals unit in calculus are the following:

I can calculate and use the area between two curves.

I can use the disc and washer methods to calculate and use the volume of a solid.

I can use the shell method to calculate and use the volume of a solid.

I can calculate and use volumes of solids created by known cross sections.

During the lesson focusing on the first goal, we used a scenario from a TImath activity The Area Between to start our conversation.

I rarely send the TNS documents as is to my students or give them a copy of the printed student handout (even though I learn from both in my own planning of how the lesson will play out). This activity gave the following information on the first two pages:

Suppose you are building a concrete pathway. It is to be 1/3 foot deep.

To determine the amount of concrete needed, you will need to:

– calculate area (the integral of the top function minus the bottom function

– calculate volume (area multiplied by depth)

The borders for the pathway can be modeled on the interval -2π ≤ x ≤ 2π by

f(x)=sin(0.5x)+3

g(x)=sin(0.5x)

On the next page, graph the functions. Use the Integral tool to calculate the area under f1 and f2. Then, use the Text and Calculate tools to find the volume of the pathway.

Which takes away any opportunity for students to engage in productive struggle.

I shared this instead:

Suppose you are building a concrete pathway that is to be 1/3 foot deep. The borders for the pathway can be modeled on the interval -2π ≤ x ≤ 2π by f(x)=sin(0.5x)+3 and g(x)=sin(0.5x).

(I’m fully aware that giving them even this much information takes away from the modeling process … but there is always give and take, and for this lesson, the learning goal wasn’t whether they could determine functions for modeling the sidewalk.)

They decided to graph the functions.

And talked about how they could calculate the area between the curves.

They had never used the Integral tool for graphs, much less the Bounded Area tool, so they oohed and aahed gasped in amazement.

Sydney asked: Is that the only way to get the area between the curves?

(I knew that she was looking for and making use of structure, composing and decomposing the sidewalk into regions with equal area).

I answered: Is it?

We made Sydney the Live Presenter, and she used the Integral tool to calculate the area between f(x)=sin(0.5x)+3 and the x-axis from -2π to 2π.

So how can we calculate the amount of concrete needed? The integral and bounded area tools are helpful for visualizing what you’re calculating, but you can’t use those tools on the AP Exam.

And so the students decided to calculate the area between the curves and then multiply by 1/3 to get the volume of the pathway.

Because they were able to tell me what to do, I almost didn’t send a Quick Poll to collect a definite integral that would calculate the volume. I wanted to hurry up and get to a card-matching activity similar to Michael Fenton’s that I knew would be helpful, but instead I eased the hurry syndrome and sent the poll.

What I saw and heard was well worth the time that it took.

Can you spot the students’ misconception?

Several students were multiplying the definite integral by 4π and by 1/3, to represent height times base times depth, instead of recognize that the definite integral represented height times base (area), and not just height. (They knew this … we had summed the areas of an infinite number of rectangles for a certain base to calculate area under the curve. But they obviously didn’t know this like they needed to.)

When we calculated their integral, we didn’t get (1/3)*37.699, as expected.

 

Next I purposefully choose a region for which the upper and lower boundaries changed.

We had a nice look for and make use of structure discussion about different ways to write a definite integral for calculating the area of the region.

Many of you might notice that there is more opportunity to look for and make use of structure for the concrete pathway. I never asked whether you really need calculus to calculate the volume of the pathway. Nevertheless, I feel like I found two good problems/items/tasks to push and probe student thinking. And there’s always next year, as the journey continues …

 

A New Function

One of the NCTM Principles to Actions mathematics Teaching Practices is support productive struggle in learning mathematics. In the executive summary, we read “Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships.”

In calculus, we started the semester with a unit on Transcendental Functions. On the first day, students figured out everything they could about F(x).

What is F’(x)?

What is F’’(x)?

What is F(1)?

Where is F(x) increasing, decreasing?

Where is F(x) concave up, concave down?

What is the domain for F(x)? the range?

Then they sketched a graph of F(x) from what they figured out, and determined that F(x)=ln(x), and F’(ln(x))=1/x.

(I found the suggestion for students coming up with F(x)=ln(x) by thinking through these questions somewhere else. But I don’t remember where, and I can’t find it anymore.)

 

So the next day, I asked them to differentiate y=log(2x).

I had not given them any “formula” for differentiating logarithmic functions. They had only figured out that the derivative of ln(x) was 1/x.

I sent the question to them as a Quick Poll to watch their progress.

I watched for a long time.

I saw and I heard productive struggle.

And eventually, their struggle turned into success.

We can cover so many more examples when we don’t give students time to grapple with mathematical ideas and relationships. But how effective are the examples without the productive struggle?

Ultimately, are my students better off having struggled to think through change of base to get to the derivative of log(2x) using what they already know about the derivative of ln(x)? Or would they have been better off with me giving them the textbook way to calculate the derivative of log_b(x)?

I’m hoping for the former, as the journey continues …

 

Productive Struggle: The Law of Sines

NCTM’s Principles to Actions suggests eight Mathematics Teaching Practices for teachers. One of them is to support productive struggle in learning mathematics. The executive summary states: “Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships.”

What does productive struggle look like? What does it sound like?

I saw a glimpse of what productive struggle looks like yesterday. I get to share a room with a teacher (who happens to be a former student of mine), and so I listen with one ear when I’m in the room working at my desk during her Precalculus class. The lesson was on the Law of Sines, but Trisha didn’t tell the students from the beginning that was the learning goal. Instead, the students focused on the math practice make sense of problems and persevere in solving them.

She presented a situation. And the students made assumptions and asked questions.

One I remember hearing was “I guess we can’t just use a measuring tape?”

Then she asked them to solve the problem.

And so they did. These students didn’t balk at the task. They all worked. They didn’t even talk very much at first … you could hear them thinking in the silence that encompassed the room. That’s when I looked over and realized that I was seeing productive struggle in action. Productive struggle isn’t always quiet, but it definitely started that way for these students. Eventually, students listened to Ain’t No (River Wide) Enough while they worked.

When solving the non-right triangle without knowing the Law of Sines, the students used another Math Practice – look for and make use of structure – to draw auxiliary lines. Some drew an altitude for the given triangle to decompose it into two right triangles. Some composed the given triangle into a right triangle.

 

Trisha collected evidence of what students could do using a Quick Poll.

So if we are given one side length and two angle measures of a triangle, is there a faster way to get to the other side?

More productive struggle … the numbers are now gone, students are reasoning abstractly to make a generalization.

And they did.

And they derived the Law of Sines in the meantime.

How often do we give our students a chance to engage in productive struggle? In how many classrooms is the Law of Sines just given to students to use, devoid of giving students the opportunity to “grapple with mathematical ideas and relationships”?

When I discussed what I saw with Trisha, she noted that last year, only a few of the students in her class successfully solved the triangle prior to learning about the Law of Sines. This year, all of them tried and most of them succeeded. These are the students with whom we started CCSS Geometry year before last. These are the students who have been learning high school math with a focus on the Math Practices. These are students who are becoming the mathematically proficient students that we want them to be. Because we are letting them. As the journey continues, we are learning to leave the front of the classroom behind so that we can support productive struggle in learning mathematics.

 

Systems of Equations – Take 3

What do you do with Systems of Equations in a high school Algebra 1 class?

Our students have some experience with systems from grade 8, but not as much as they eventually will with full implementation of our new standards.

NCTM’s Principles to Actions lists Establish mathematics goals to focus learning as one of the Mathematics Teaching Practices. We can tell that having a common language to talk about what we are doing is helping our students communicate to us about what they can and can’t (yet) do.

We started our unit on Creating Equations & Inequalities with the following leveled learning progression and questions:

Level 1: I can determine whether an ordered pair is a solution to a linear equation.

Level 2: I can graph a linear equation y=mx+b in the x-y coordinate plane.

Level 3: I can solve a system of linear equations.

Level 4: I can create a system of equations to solve a problem.

 

NCTM’s Principles to Actions lists Elicit and use evidence of student thinking as one of the Mathematics Teaching Practices. We need to know what students are thinking so that we can move their thinking forward. We created a leveled learning formative assessment so that we could see where students are.

Level 1: I can determine whether an ordered pair is a solution to a linear equation.

 

 

We have this y= Question configured to generate a graph preview. The equations students enter graph as they are typed, so the students are able to check their thinking as they go. (Note that we don’t have to configure the question to graph the equation as it is entered; we are choosing to do so while students are learning.)

The following are the results from one of our Algebra 1 classes. This is my favorite question.

How can we use the equation to know whether it contains the point (2,3)?

How can we use the graph to know whether it contains the point (2,3)?

What happens when we give students a point & ask them to create two equations that contain the point?

Do they know that they are creating a system?

Does it help them to know that eventually we will give them the equations and ask them for the point?

 

Level 2: I can graph a linear equation y=mx+b in the x-y coordinate plane.

And results from the second question:

Level 3: I can solve a system of linear equations.

What’s significant about the green point?

What does it have to do with the given equations?

 

At least half of our students don’t yet understand what the solution is.

 

 

And only a very few are able to solve the system from the question on 3.3, which is okay. This is the first day of the unit. We have the information we need to know how to proceed with the lesson.

 

 

I wrote about some of the tasks we used on the first two days of the unit here.

On the third day, we tried Dueling Discounts from Dan Meyer’s 101 Questions, which went better than Dan’s Internet Plans Makeover.

And more:

 

Maybe it’s time to generalize our results?

On the last day we tried Candy & Chips from 101 Questions, which also went well.

NCTM’s Principles to Actions lists Build procedural fluency from conceptual understanding as one of the Mathematics Teaching Practices. We know we aren’t there yet, but we are definitely making progress as the journey continues …