Trig Ratios

How do your students experience learning right triangle trigonometry? How do you introduce sine, cosine, and tangent ratios to them?

NCTM’s Principles to Actions includes build procedural fluency from conceptual understanding as one of the Mathematics Teaching Practices. In what ways can technology help us help our students build procedural fluency from conceptual understanding?

Until I started using TI-Nspire Technology several years ago, right triangle trigonometry is one topic where I felt like I started and ended at procedural fluency. How do you get students to experience trig ratios?

I’ve been using the Geometry Nspired activity Trig Ratios ever since it was published. Over the last year, I also read posts from Mary Bourassa: Calculating Ratios and Jessica Murk: Building Trig Tables about learning experiences for making trigonometric ratios more meaningful for students. Here’s how this year’s lesson played out …

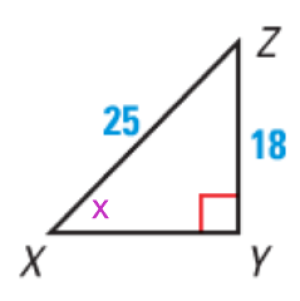
We first established a bit of a need for something called trig (when they finally get to learn about the sin, cos, and tan buttons on their calculator that they’ve not known how to use). I showed a diagram and asked how we could solve it. We reserved “trig” for something they couldn’t yet solve.

We use TI-Nspire Navigator with our TI-Nspire handhelds, and so I can send Quick Polls to assess where students are. Sometimes Quick Polls aren’t actually so “quick”, but these were, along with letting students think about what we already know and uncovering a few misconceptions along the way (25 isn’t the same thing as 18√2).

Next I asked each student to construct a right triangle with a 40˚ angle and measure the sides of the triangle.

I sent a Quick Poll to collect their measurements.

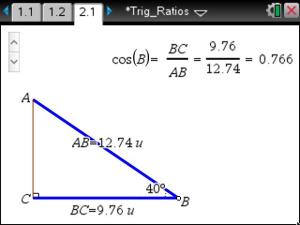
Then we looked at the TNS document for Trig Ratios. Students can take multiple actions on the diagram. I asked them to start by moving point B. What do you notice? We recorded their statements for our class notes.

Then I asked them to click on the up and down arrows of the slider. What do you notice?

What ratio of side lengths is used for the sine of an angle?

You all constructed a right triangle with a 40˚ angle and recorded the measurements. What’s true about all of your triangles?

• The triangles are all similar because the angles are congruent.
• The corresponding side lengths are proportional.
• We know that sin(40˚) is always the same.
• So the opposite leg over the hypotenuse will be the same?

Will it? We sent their data to a Lists & Spreadsheet page and calculated a fourth column, opp_leg/hyp. What do you notice?

Of course their ratios aren’t exactly the same, but that’s another good discussion. They are close. And students noticed that one entry has the opposite leg and adjacent leg switched because the leg opposite 40˚ is shorter than the leg opposite 50˚.

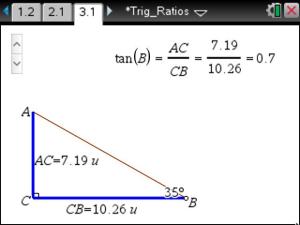
We didn’t spend long looking at the TNS pages for tangent and cosine … students were well on their way to understanding a trig ratio conceptually. They just needed to establish which side lengths to use for cosine and which to use for tangent.

There’s a reason that #AskDontTell has been running through my mind as I have conversations with my students and reflect on them. Jill Gough wrote a post using that hashtag over two years ago: Circle Investigation – #AskDontTell.

What #AskDontTell opportunities can you provide your students this week?

[Cross-posted at T3 Learns]