How do you give your students the opportunity to practice MP8: I can look for and express regularity in repeated reasoning?

We started our dilations unit practicing MP8, noticing and noting.

What would you want students to notice and note?
How do students learn what is important to notice and note?
An important consideration when learning with self-explanation is to look at the quality of the explanation itself. What are the students saying or writing? Are they just regurgitating bits of text or making connections to underlying principles? Do the explanations contain predictions about what is going to happen, try to go beyond the given instruction or do they just superficially gloss over what is already there? Students who make principle-based, anticipative, or inference-containing explanations benefit the most from self-explaining. If students seem to be failing to make good explanations, one can try to give prompts with more assistance. In practice, this will likely take iteration by the instructor to figure out what combination of content, activity and prompt provides the most benefit to students. (Chiu & Chi, 2014, p. 99)
We had a brief discussion about what might be important to notice and note. We’ve also been working on predictions, thinking about what you expect to happen before trying it with technology:
What happens when the center of dilation is on the figure, outside the figure, and inside the figure?

What happens when the scale factor is greater than 1? Equal to 1? Between 0 and 1? Less than 0?

I observed, walking around the room and using Class Capture, selecting conversations for our whole class discussion.


Here’s what NA noticed and noted.

We looked at Hannah’s Rectangle, from NCSM’s Congruence and Similarity PD Module. Students had a straightedge and piece of tracing paper.
Which rectangles are similar to rectangle a? Explain the method you used to decide.

What would you do next? Would you show the correct responses? Or not?
Would you start with an incorrect answer? or a correct answer?
Would you regroup students based on their responses?

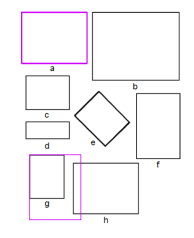

I started with a student who didn’t select G and then one who did. Then I asked a student who selected C to share why he chose C and didn’t choose F. We ended by watching Randy’s explanation on the module video.
And so the journey continues, always wondering what comes next (and sometimes wondering what should have come first) …
Chiu, J.L, & Chi, M.T.H. (2014). Supporting self-explanation in the classroom. In V. A. Benassi, C. E. Overson, & C. M. Hakala (Eds.). Applying science of learning in education: Infusing psychological science into the curriculum. Retrieved from the Society for the Teaching of Psychology web site: http://teachpsych.org/ebooks/asle2014/index.php
