Calculating Area – Looking for and Making Use of Structure

Several months ago when I was preparing a session on Geometric Measure & Dimension for the Mississippi Department of Education Geometry Institute, I noticed a blog post by Kate letting us know about some new IM tasks. Areas of Special Quadrilaterals (and one triangle) caught my attention, and so I took a look. I had no idea at the time how perfect this task was for starting the session.

Jill Gough and I often talk about pairing a content standard with a practice standard.

For this activity, the content standard was 6.G.A.1:

Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.

And the practice standard was look for and make use of structure.

How would you find the area of each figure, composing into rectangles or decomposing into triangles and other shapes?

Many teachers used color to make their thinking visible. I learned quickly, however, not to assume that they had found the area a certain way just because of a certain auxiliary line. I walked around, asking about their thinking, selecting and sequencing for our whole group discussion.

We started with figure a.

Some decomposed into a rectangle and two triangles.

Some decomposed into unit squares.

Some composed into a rectangle to think about the areas of the two small triangles.

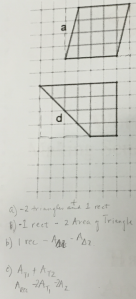
Others decomposed into a rectangle and two triangles but then rearranged the two triangles into a rectangle.

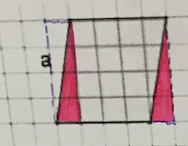
Others translated one triangle horizontally to rearrange into one rectangle.

One lady had not taught geometry for a very long time. She said she thought she knew a formula that would work for calculating the area, but she wasn’t confident about her work. Her formula? A=½h(b₁+b₂). Most participants knew that formula as the area of a trapezoid. Does it work for the parallelogram? They tried it. It worked. Maybe that adds to our reasons for considering the inclusive definition of trapezoid?

We looked next at figure d.

Some composed into a rectangle and subtracted the area of the right triangle.

Some decomposed into a triangle and rectangle.

One decomposed into a triangle and parallelogram.

Some decomposed into unit squares.

Some decomposed and rearranged into a rectangle.

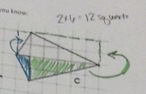
Then we looked at figure c.

So many ways!

Composing into a rectangle. From there, some subtracted the area of each right triangle. Some halved the area of the rectangle.

Decomposing into triangles. Some into 4 triangles with both diagonals. Some into 2 triangles with the vertical diagonal. Some into 2 congruent triangles with the horizontal diagonal.

Some decomposed and rearranged.

Everyone practiced look for and make use of structure in ways they hadn’t thought to before. Everyone worked on their mathematical flexibility to find more than one way to determine the areas of the figures. Everyone learned at least one new way to look at the figure from the others in the room.

What opportunities do you provide your learners to look for and make use of structure and then share what they’ve made visible that wasn’t pictured before?