Vertical Angles Are Congruent

CCSS-M.G-CO.C.9. Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints.

How do we know that vertical angles are congruent, other than “my teacher told me”, or “the dynamic geometry software convinces me”. (Even though we did let our dynamic geometry software convince us, as most students had not before seen measured vertical angles move.)

Students worked individually first. I monitored their work.

How many times have you heard a student say that they don’t know where to start when writing a proof?

Can the leveled learning progression that Jill Gough (@jgough) and I have written for construct a viable argument and critique the reasoning of others help?

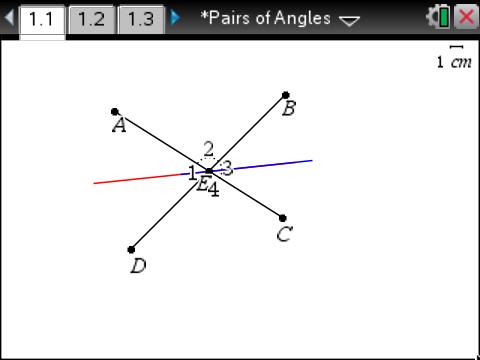
What information is given (or implied) in the diagram?

One student marked given information on the diagram so that she could understand it.

Another student is on her way to establishing given information and is working on communicating why her conjecture must be true.

Another student uses his given information and can get to m∠2=m∠4 but should probably show that m∠2+m∠3=m∠3+m∠4 more directly.

Without realizing it, another student is on her way to establishing the Congruent Supplements Theorem. We can see from her work that she used some angle measures to make sense of why vertical angles have to be congruent.

And another student with a “congruent supplements” argument but not written exactly the same way.

So 1 of the 31 students suggested that vertical angles are congruent because of a reflection.

What information do we need to know to define a reflection?

An object and a line.

So about what line are you reflecting ∠2 or ∠4 to show that the figures are congruent?

By the time I had made it around the room again, TL had decided that the angles should be reflected about the angle bisector of ∠3 and ∠1.

When we were ready for the whole class discussion, we started with the progression of traditional Euclidean proofs – letting each student I called on adding a bit more to the argument. Then we considered TL’s proof with rigid motions.

His argument makes sense to the class – and in fact if we test the conjecture using technology we can see that it is true:

But I wonder how we can prove the angle bisector of ∠1 is collinear with the angle bisector of ∠3 without technology. Maybe an indirect proof would work?

So is there another rigid motion that would let us show the congruence of vertical angles?

A rotation?

A rotation of what object about what point using how many degrees?

And so, together, we came up with the following argument to show that vertical angles are congruent using a rotation.

And so the journey continues … learning more about transformational geometry every day from my students, who see geometry unfold differently than I, because their study of geometry started with rigid motions.