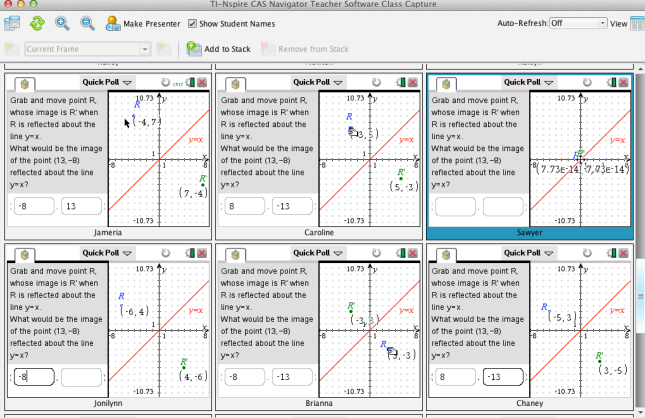
Students had the opportunity to look for and express regularity in repeated reasoning while reflecting a point about the line y=x.
I sent an interactive Quick Poll so that they could move the point, observe its reflection about y=x, and then determine the image of a point not shown on the graph.
Then I asked students to generalize their results by determining the image of (a,b) reflected about y=x. Which responses would your students accept as correct?
Students had a more difficult time reflecting a point about the line y=–x. 18 of 26 got it correct for the Quick Poll on which they “played”. (Show Correct Answer has been deselected.)
But only 12 got it correct for the Quick Poll that simply asked the question.

Would a graph help?
Drawing a representation of the situation is not yet second nature.
Then we reflected a point about the horizontal line y=–2 first on the graph:
And then we reflected a point about the vertical line x=2 on the graph:
Next, I didn’t give them a graphical representation.
But more of them thought to create their own.
And then the bell rang while students were submitting.
And so the journey to provide students opportunities to develop mathematical habits of mind continues …