Seven Circles I is (obviously by the name) one of several tasks on the Illustrative Mathematics site about seven circles.
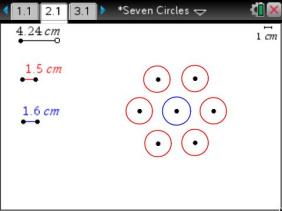
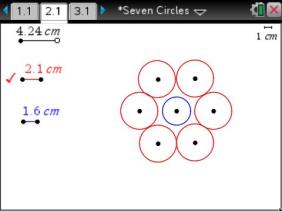
Liz places seven pennies in the arrangement shown. She notices that each of the six outer pennies touch the one in the center and its two outer neighbors. Liz wonders whether or not this is true if the pennies are replaced with seven nickels or quarters or, more generally, any set of seven equally sized circles. What is the answer to Liz’s question, that is, is it possible to place six circles around a central circle so that each outer circle touches the one in the center as well as its two outside neighbors?
Our student responses to this task were mildly interesting. Most didn’t have time to delve deeply into the problem because it was the last performance assessment task we asked them to consider after two others (posts to come), but a few were worth noting.
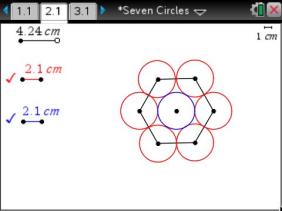
Only one student got at the true mathematics underneath the reason that the original arrangement works. The sample solution on the site actually suggests that the teacher might want to provide the students some guidance as to what to consider – the auxiliary lines that might be helpful in considering an actual solution to the problem – and not just an agreement that the arrangements works with any congruent circles because of a dilation of the original picture with pennies.
I wonder, though, what would happen if students started with a different question.
Is it possible to start with a center circle and place six outer circles tangent to each other and the center circle? Under what conditions will it work?
What about placing five outer circles tangent to each other and the center circle? Under what conditions will it work?
Will it work with four outer circles tangent to each other and the center circle?
Or seven?
Or n?
I just spent more time than I had exploring this problem. I ended up finding the diameters of U.S. coins and even figured out that it will almost work to place a nickel in the center of the configuration and five half dollars around the nickel, tangent to each other and the nickel.
I was glad to have a CAS to help with the solving so that I could focus on modeling and whether my solutions made sense.
And I was glad for a TNS document that Jeff built to model this problem so that I could check my work.
Or what would happen if students came up with their own questions regarding the arrangements of circles around a circle. I just got Make Just One Change: Teach Students to Ask Their Own Questions, but I haven’t started reading it yet. From some of the comments on the papers that I read, I think that some students would want to explore the area of the space in the arrangement that is not covered by a circle.
I’m not sure we will get to come back to this problem this year, but I will look forward to next year, as the journey continues ….











One response to “Seven Circles”