Angle Proofs

CCSS-M Congruence G-CO 9

Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints.

How do you go about having students prove theorems about lines and angles in your class? We certainly don’t formally prove every theorem in our geometry course that we use, but we prove a lot of them. What we do that I believe is more important than proving theorems is exploring the hypothesis to make sense of possible conclusions. I remember memorizing a lot of theorems out of our geometry textbook when I took high school geometry. I don’t think that is what my students will remember from our class. In fact, I know it is not.

So bear with me as I share two student reflections about the course:

“I have never really liked math and wasn’t looking forward to this class because of it. Surprisingly, I actually like it much better than I thought I would. Although geometry has confused me sometimes this year, I have actually felt proud when I figure something out that I thought I couldn’t. I think I have been able to get a new mindset and have been able to switch from thinking regularly to analytically when I enter your class. I can now look at a problem, and try to think about it in different ways until I figure out how to solve it.”

“The main memory that I will keep of Geometry class is so complex that everything I say will simply be an understatement.  Although I will attempt to describe it.  The main memory I will keep of this class is the memory of the first math class that I enjoyed.  I liked the fact that in that class I sometimes had the bravery to answer questions.  I was not nervous to have the wrong answer in front of the class or Mrs. Wilson.  I loved the fact that Mrs. Wilson incorporated enjoyable activies throughout her lessons. This was the first math class I really engaged myself in.”

So we make a big deal about accepting postulates and proving theorems in our class deductive system for geometry. We looked at a list of Euclid’s axioms and postulates and noted that Euclid’s 5^th postulate took way longer to make sense of than any of the others.

And then we set out to prove theorem #1.

Vertical angles are congruent. Most of my students know that vertical angles are congruent. But they have not thought about why vertical angles are congruent.

What do we know to be true in this diagram? Students noted that the sum of angles 2 and 3 is 180°. The sum the sum of angles 3 and 4 is 180°. Students noted that the sum of angles 1, 2, 3, and 4 is 360°. How do we know this? We can observe it using technology. We used the angle measurement tool to verify the measures of other angles in the diagram. But how do we know it will always be true? So we proceeded to formalize that vertical angles are congruent … making use of the Angle Addition Postulate that we had agreed to accept into our deductive system without proof. And making use of Euclid’s axioms – if equals are subtracted from equals, the remainders are equal – that we now call the Subtraction Property of Equality. Eventually we proved that angles 2 and 4 were congruent.

Next I sent students a Quick Poll: ∠3 and ∠2 are both supplementary to ∠1. If m∠3=50°, what is m∠2?

And asked them to make a conjecture: If two angles are supplementary to the same angle, then …

And then we proved that if two angles are supplementary to the same angle, then they are congruent to each other..

Given: ∠2 is supplementary to ∠1. ∠3 is supplementary to ∠1.

Prove: ∠2≅∠3

What about the converse?

Is it true?
It didn’t take students long to decide that it wasn’t true. Their counterexample was to suppose m∠2=m∠3=180.

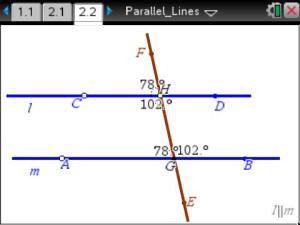
So we moved next to parallel lines, remembering Euclid’s 5^th postulate as we began to explore what happens when parallel lines are cut by a transversal.

What can we conclude about lines a and b? lines m and n?

We agreed that when corresponding angles are congruent, the lines are parallel. Do we agree enough to let this in to our deductive system as a postulate?

I heard from another geometry teacher that her students thought of corresponding angles as a translation, which goes right along with figures being congruent if there is a rigid motion that maps one onto the other…and a good reason for us to communicate with each other about what we do and say in the classroom. That idea hasn’t come up in my classroom yet, but I will make sure that it does.

And so from there, we proved that alternate interior angles are congruent when parallel lines are cut by a transversal. We didn’t prove that alternate exterior angles are congruent, since the proof is similar. We proved that consecutive interior angles are supplementary when parallel lines are cut by a transversal. We didn’t prove that consecutive exterior angles are supplementary, since the proof is similar.

And then on the summative assessment, I asked the following, which I believe gave evidence that students are beginning to learn to create arguments and they are not just memorizing proofs to recreate on a test.

Suppose you are structuring your deductive system in such a way that you postulate the following about alternate interior angles:

If two parallel lines are cut by a transversal, then alternate interior angles are congruent.

Prove the Corresponding Angles Theorem using the Alternate Interior Angles Postulate and without using results from any parallel line theorems that we proved in class.

Our last part of parallel lines was specifically to think about auxiliary lines. The progression of questions follows.

  

I am not convinced that I did them in the right order, although maybe it is significant that all but one student got the 3^rd problem correct. Should we have started with the 3^rd problem instead of the 1^st? Since we did start with the 1^st, the effect was subtle for problem #3. Many students drew immediately drew auxiliary lines when they saw the 3^rd problem. After the 3^rd problem, I drew my students’ attention to the math practice look for and make use of structure, which explicitly states drawing auxiliary lines to support an argument. Student shared their thinking, as their arguments for finding the measure of angle 3 were not all the same.

Are we wasting our time proving a few of these theorems in class? We don’t write formal two-column proofs for every theorem that we prove, but we do come up with a logical argument as to why the theorems are true. What we do is reason abstractly and quantitatively. What we do is construct a viable argument and critique the reasoning of others. My students recognize that we are figuring out geometry instead of being told geometry, whether they appreciate it yet or not.

And so the journey continues …